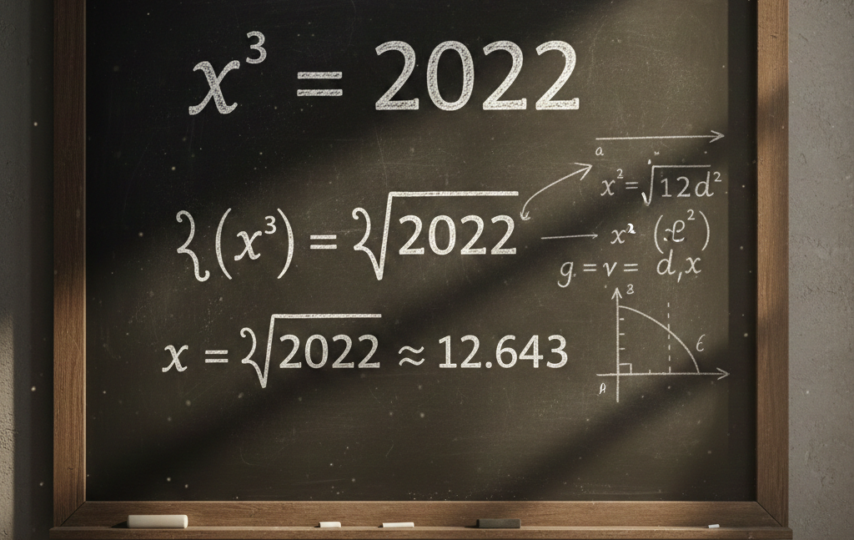The solution of the given cubic equation is roughly 12.65. 

The problem of locating a number x such that x*x*x is equal to 2022 is great mathematical test. It challenges us to trace out the operations of reason until the unknown yield.

What appears so daunting at a glance is easily handled when we realize that it is a cubic relation. In order to find the figure X that satisfies the condition x*x*x is equal to 2022, we have to find the root that will not contradict the equation. 

Step-By-Step Numerical Techniques for Approximating x

Individuals who are well informed on such issues rarely anticipate that the solution will be found in a flash. Rather, they start with a rough estimate, calculate the difference between the estimate and the target value and change their value based on this difference. This is repeated, trial, correction, till the value stabilizes. The solution is found in this gradual diminishing of possibilities.

Advanced Computational Methods for Exploring Cubic Roots

Possibilities can be tried at rates that no individual could handle single-handedly using numerical routines and well-crafted programs. Using these aids, one can go through a large number of candidates of x until the value that fulfills the relation comes out with certainty.

Uncovering Exact Forms Through Symbolic Algebra

Occasionally the equation provides not only an approximation but also a form that can be expressed in an exact form. In those situations, algebra provides a collection of methods such as careful rearrangement, gradual reduction, and use of known identities to unravel each layer of the problem. By this patient handling, it is possible to isolate x and express the solution in its precise form.

Real vs. Complex Solutions in Cubic Equations

A cubic equation possesses its own strange ways. It can have one real solution, or it can give three, according to the behavior of its discriminant. Sometimes the rest of the roots will wander into the world of the imaginary numbers, and expand the base on which the problem is founded. By taking care of the character of these roots one enriches their perception of the equation and sees how extensive the area of mathematics may become when pursued to the furthest extremes.

Real-World Applications of Cubic-Root Problems

The number whose cube is 2022 is sought further than one branch of study. Such issues are found in the sciences, in engineering, and in the task of computation; all of these disciplines use such equations to describe or model the world around us. Through wrestling with them, we assist in laying the foundation of advancement in most types of inquiry. 

Whether by repeated trial, by specialized methods, or by the careful manipulation of symbols, the task will tend in the same direction, to the figures which will satisfy the equation. The work makes us better understand the principles on which they are based, and it gives back the feeling of curiosity which makes mathematical discovery more than a calculating-machine. 

Conclusion

In our search of solving x*x*x is equal to 2022, we are reminded that there are equations that just like to be a little difficult to solve. It is no epic of the sort that Fermat wrote about his famous riddle, but this unusual cube puzzle demonstrates that mathematics is not about the end value alone, but about the journey that we make to get there.   

You may like the old-fashioned look of having to scribble through the calculations or you may be happy to have a machine do the work and crunch the numbers (and yes, it settles around x≈12.65) but the best part of it is the doing.

FAQs

Q1: What is the equation x³ = 2022 really asking me to figure out?

It is just requesting you to find the number that yields 2022 when multiplied 3 times with itself. Imagine that you are solving, backwards, a cube: You are trying to reverse the process and find the side length which will give you a volume of 2022. The mystery value falls near 12.65.

Q2: Why can’t I just punch this into a calculator and call it a day?

Yes, you can and we will not judge! Yet there is something strangely satisfying about the process of getting to know how the answer is arrived at, by iterative guessing, by algebraic magic, or by brute force of computation. It is the difference between heating up food in the microwave and preparing it: they both will give you something to eat, but only one will give you the rights to boast about. 

Q3: Do cubic equations really matter outside of textbook problems?

Absolutely. They are manifested in all kinds of real life situations. Engineers use cubic relationships when processing the volume and structural calculations, physicists use them in the analysis of changing motion, and computer scientists encounter them in the design of algorithms and in the modeling of data. Equations such as this one are crucial parts of all kinds of construction and environmental simulations and even the technology behind your streaming recommendations.